Lecture 06 - Local Search

#notes#cs471

Recap §

Best First Search §

• When deciding which node to expand next, choose node n with minimum value of some evaluation function f(n)
• Priority Queue ordered from low to high by f Example:
• Breadth first search: Expand shallowest node first
  • f(n) = Depth(n)

Informed Search §

• Search algorithm uses domain specific hints about goals
• Hints formulized from heuristic function h(n)
• h(n) = estimated cost of cheapest path from n to a goal state.
• Idea: Best first search that contains h(n)

Heuristic Function §

• Non-negative function that estimates how close a state is to a goal.
• h(n) = 0 if n is a goal state.
• Examples include Manhattan Distance, Euclidian Distance, etc. for path planning.

A* Search §

• $f(n)=g(n)+h(n)$

Optimality of A* Search Tree §

1. $f(n)\le f(A)$
   • $f(n)\le g(n)+h^{\ast }(n)=g(A)$
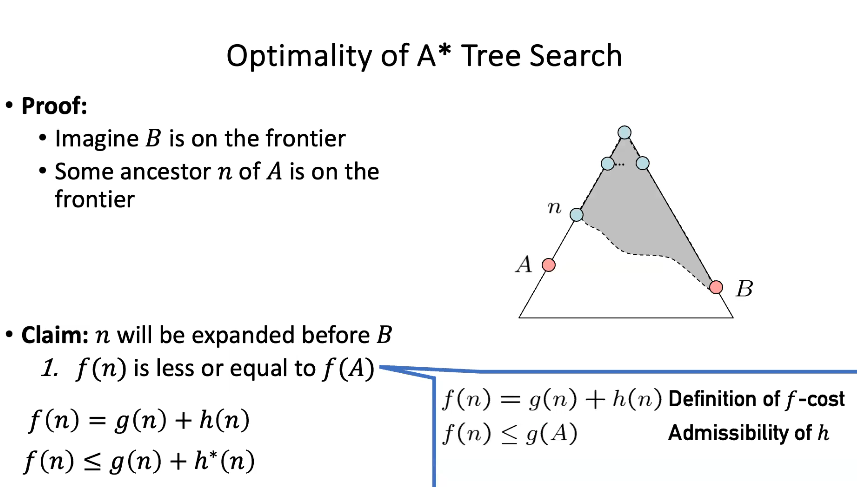
2. $f(A)$ is less than $f(B)$
3. $n$ expands before $B$

• All ancestors of A will expand before B
  • A expands before B
  • A* search is optimal

Consistency of Heuristics §

Main Idea: estimated heuristic costs $\le$ actual costs

• Admissibility §

  • Heuristic Cost $\le$ actual cost to goal
  • $h(n)\le$ actual cost from n to G

• Consistency §

  • heuristic ‘arc’ cost $\le$ actual cost for each arc
  • $h(n)-h(n^{\prime })\le cost(nto{n}^{\prime })$
  • $h(n)\le cost(nto{n}^{\prime })+h(n^{\prime })$

Search and Models §

• Your search is only as good as your models.

From Path-Based to Local Search §

• So far we have considered search methods that:
  • Systematically explore full search space
  • Return path from start to goal
• In many problems path is irrelevant; goal is all you care about
  • Ex. 8 queens problem
• Sometimes the goal test itself is unclear.
  • Ex. optimization problem (you don’t know best value)
  • Travelling salesman.

Local Search §

• Useful when path to goal state does not matter
• Basic Idea:
  • Only keep single “current” state
  • Improve iteratively
  • Don’t save paths followed
• Characteristics
  • Low memory req
  • Effective — can find solutions in large spaces

Eight Queens Problem §

• Place 8 queens on board such that none can attack one another
• How to formulate search?
  • Incremental formulation
  • Complete-state formulation
• Heuristic / Objective: Number of attacking queens

Hill Climbing Search §

• Consider state-space landscape where:
  • Location = state
  • Elevation = evaluation of state
• Move towards direction of increasing ‘value’

function HillClimbing(problem) return a state that is a local maximum
 current <- initial_state
 repeat:
	 best_neighbor <- current
	 for state in Neighbors(current):
		 if state.value > best_neighbor.value:
			 best_neighbor <- state
	if best_neighbor > current.value:
		current <- best_neighbor
	else:
		return current

Challenges for hill-climbing §

• Local Maxima
  • No way to back track from a local maximum
• Plateau
  • Can have difficult time finding a way off flat portion of state space
• Ridges
  • Ridges produce series of local maximum that are difficult to navigate out of

Variants of local hill-climbing §

• Stochastic hill-climbing
  • Select randomly from all moves that improve the value of objective function.
• Random-restart hill-climbing
  • Conduct series of hill-climbing searches from random positions
  • Very frequently used in AI

Simulated Annealing §

• Key Idea: mostly goes “uphill” but occasionally travels “downhill” to escape local optimum
  • Likelihood to go downhill is controlled by a “temperature schedule”

function SimulatedAnnealing (problem, schedule) return a solution state
current <- initial_state

from t = 1 to infinity:
	T <- schedule(t)
	if T = 0 then return current
	next <- a randomly selectd neighbor of current
	dE = next.value - current.value
	if dE > 0:
		current <- next
	else:
		current <- next with probability e^{dE/T}

Local Beam Search §

• Similar to hill-climbing but…
  • Keep track of k current states, rather than single
  • Select k best neighbors among of the k current states
• Stochastic Beam Search - Successors at random weighted by value

Genetic Algorithm §

• Fitness Function
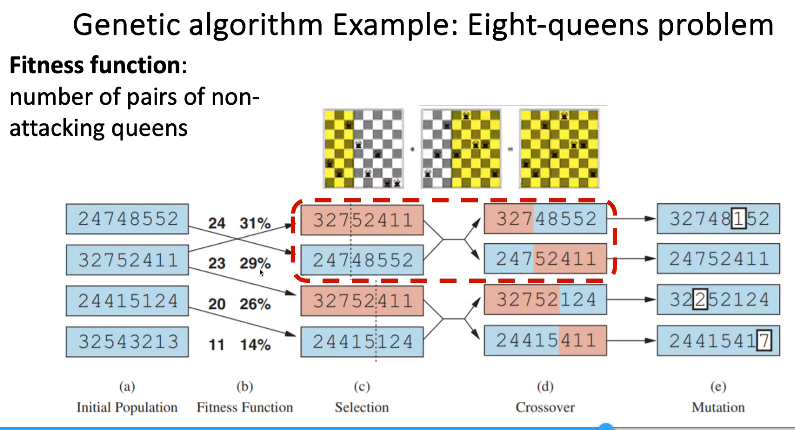
  • Ex. number of pairs of non-attacking queens

Applications §

Bounding Box Prediction §

Object Detection: Single Object Idea: Check all boxes, find the most “cat”

• About H x W positions
• ~H x W window sizes

Hill Climbing Search §

• $ma{x}_{box}f(Image,box)$
• How to represent state?
  • Bounding Box:
    • Top-left and bottom right corners
    • $(x_1,y_1.x_2,y_2)$
  • How to define neighborhood?
    • $(x_1+1,y_1.x_2,y_2)$
    • $(x_1-1,y_1.x_2,y_2)$
    • $(x_1,y_1+1.x_2,y_2)$
    • $(x_1,y_1-1.x_2,y_2)$
    • …

Example §

Problem:

• Place airport such that sum of squared straight-line distances from each city is minimized. Formulation:
• Location of airport $x=[x_1,x_2]$
• Cost function
• $f(x)={\sum }_{i=1}^n(c_{i,1}-x_1{)}^2+(c_{i,2}-x_1{)}^2$ How to handle continuous state?
• Discretize into intervals of $\delta$ (delta)
• Local search with Empirical Gradient
• $\frac{(f(x+\delta )-f(x)}{\delta }$

Gradient Descent §

• 
• Move in opposite direction of gradient (steepest slope) in this situation
• 

How to choose step size? §

• Constant: $n^t=\frac{1}{L}$
• Diminishing: $n^t\to 0,{\sum }_t{n}^t=\infty (n^t=1/t)$