Lecture 07 Adversarial Search

#notes#cs471

Recap §

Recap: Local Search §

• Useful when path to goal does not matter / solving pure optimization problem
• **Basic Idea: **
  • Only keep current state
  • Improve iteratively
  • Don’t keep paths followed

Recap: Hill-Climbing Search §

• Repeat visiting neighbors, finding a local maximum

Challenges for Hill-Climbing §

• Local Maxima
  • Once local maxima reached, no way to backtrack

Recap: Simulated Annealing §

• Key Idea: Usually goes upwards, sometimes goes downward.

Recap: Gradient Descent §

• Move towards gradient of function

Games §

• Axes:
  • Deterministic vs. stochastic
  • One, two, or more players
  • Zero sum vs. general sum
  • Perfect information vs. partial information
• Algorithms need to calculate a ”strategy” (policy) which recommends a move (action) from each position (state)

Deterministic Games §

• Problem Formulation
  • States: S (start at $S_0$)
  • Players: $P=\{\mathrm{1...}N\}$ (take turns)
  • $ToMove(s)$: The player whose turn it is to move in state $s$
  • $Actions(s)$: Set of legal moves in state $s$
  • $Result(s,a)$: Transition function, state resulting from taking action $a$ in state $s$
  • $IsTerminal(s)$: A terminal test, true when game is over
  • $Utility(s,p):S\times P\to \mathbb{R}$, Final numerical value to player $p$ when the game ends in state $s$
• Solution for a player is a policy

Zero-Sum vs. General Games §

• Zero-Sum Games
  • Agents have opposite utilities
  • Can think of outcome as a single value that maximizes, and the other minimizes
  • Adversarial, pure competition
• General Games
  • Agents have independent utilitiees
  • Cooperation, indifference, competition, and more are all possible

Adversarial Search §

Single-Agent Trees §

• No adversaries
• Value of State
  • The best achievable outcome from that state

Adversarial Game Trees §

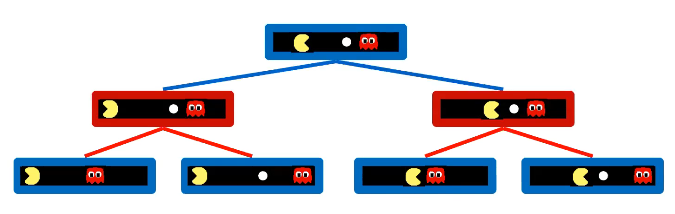
Minimax Values §

• States Under Opponent’s Control
  • $V(s^{\prime })=mi{n}_{s\in successors(s^{\prime })}V(s)$
• States Under Agent’s Control
  • $V(s)=ma{x}_{s^{\prime }\in successors(s)}V(s^{\prime })$

Adversarial Search (Minimax) §

• Deterministic, zero-sum games:
  • Tic-tac-toe, chess, checkers
  • One player maximizes result
  • Other minimizes
• Minimax Search:
  • State-space search tree
  • Players alternate turns
  • Compute each nodes minimax value )
    • Best utility against a rational (optimal) adversary

Minimax Implementation §

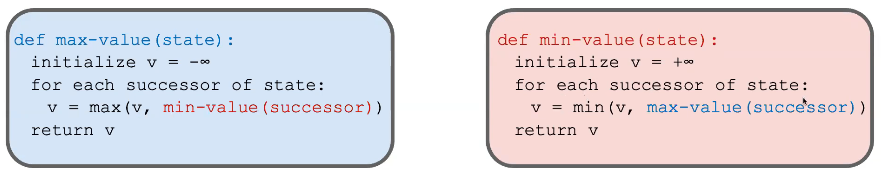
Minimax Properties §

• Optimal against a rational player. Otherwise, minimax definition of optimality may not be true

Minimax Efficiency §

• Like Exhaustive DFS
• Time: $O(b^m)$
• Space: $O(bm)$
• $b$ = legal moves, $m$ = maximum tree depth

Generative Adversarial Network §

An adversarial game of image generation

• Generator vs. Discriminator