Lecture 09 CSP I Problem Formulation and Inference

#notes#cs471

Recap §

Search/Planning: §

Sequences of actions

• Path to goal is important thing

Identification §

Assignments to variables

• Goal itself is important, not the path
• All paths at the same depth

Constraint Satisfaction Problems §

Standard Search Problems:

• State is a “black box” (arbitrary data structure)
• Goal test can be any function over states

Constraint Satisfaction Problems (CSPs) §

A special subset of search problems.

• State is defined by variables $X_i$ with values from a domain $D$
• Goal test is a set of constraints specifying allowable combinations of values for subsets of variables.
• Allows useful general-purpose algorithms with more power than standard search algs.

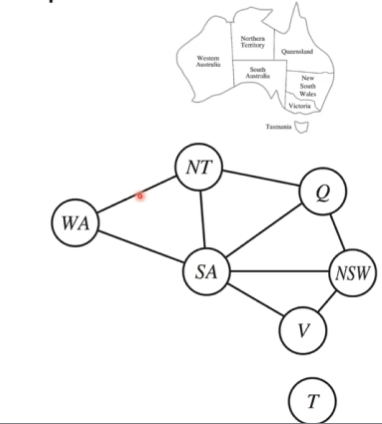
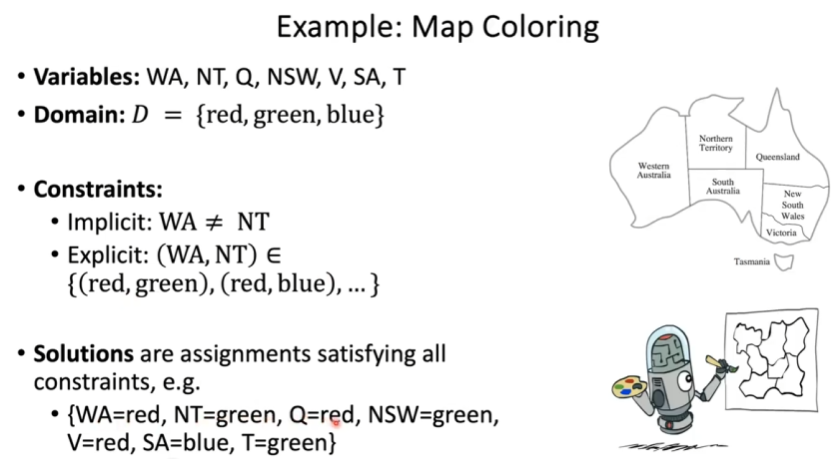
Example: Map Coloring §

• Want to color map regions certain colors (say red, green, blue), and want neighbors to NOT have the same color.
• 

Example: N-Queens §

• Variables: $Q_k$
• Domain: $D=\{1,2,3,...,N\}$
• Constraints:
  • Implicit:
    • $\forall i,j\text{NonAttacking}(Q_i,Q_j)$
  • Explicit:
    • $(Q_1,Q_2)\in (1,3),(2,4),...$

Example: Sudoku §

• Objective: Fill empty cells with numbers 1-9
• Rules:
  • Numbers appear once each row, column, and region.
• Variables
  • $v_{ij}$ is $j^{th}$ cell on $i^{th}$ row.
  • $D=1,2,3,4,5,6,7,8,9$
• Constraints
  • Row: $\forall i,{\cup }_j\{v_{ij}\}=D$
  • Column: $\forall j,{\cup }_i\{v_{ij}\}=D$
  • Block: $\forall k,{\cup }_{(i,j)}\{v_{ij}|ij\in B_k\}=D$ ($B_k$ denotes block)

Variety of CSP Constraints §

• Unary Constraints
  • Involve single variable (equivalent to reducing domains)
  • e.g. $SA\ne green$
• Binary Constraints
  • Involve pairs of variables
  • e.g. $SA\ne WA$
• Higher-Order Constraints involve 3 or more variables (e.g. Sudoku)
• Preferences (soft constraints)
  • e.g. red is better than green
  • Often represented by cost for each variable assignment
  • Gives constrained optimization problems

Constraint Graphs §

• Binary CSP
  • Each constraint relates at most 2 variables
• Binary Constraint Graph
  • Nodes are variables, arcs show constraints
• General-Purpose CSP algorithms use the graph structure to speed up search.
  • 

Solving CSPs §

Standard Search Formulaton §

• States defined by values assigned so far
• Initial State: empty assignment, {}
• Action (Successor Function): Assign a value to a unassigned variable.
• Goal Test: The current assignment is complete and satisfies all constraints.
• “Search Tree”: Explore graph using BFS
  • Problem: Inefficient, expands invalid states, reaches duplicate states

Backtracking Search §

• Idea 1: One variable at a time - Variables are expected to be commutative - Fix ordering of variables and only consider assignments to single variables at a time.
• Idea 2: Check constraints as you go
  • ”Incremental Goal Test” - Consider values only which do not conflict with previous assignments.
• 

Improving Backtracking §

• Can we detect failure early?
• Filtering: Keep track of domains for unassigned variables and cross off bad options
  • Forward Checking: Cross off values that violate a constraint when a value assignment is added to existing assignment
• Ordering
  • Which variable assigned next?
  • Which order should its values be tried?
• Structure
  • Can we exploit problem structure?

Filtering §

Consistency of a Single Arc §

• An arc $X\to Y$ is consistent iff for every x in the tail there exists some y in the head which could be assigned without violating a constraint.
• Forward Checking: Enforcing consistency of arcs from unassigned variables (i.e X) pointing to the variables with a new assignment (i.e. Y)

Arc Consistency of an Entire CSP §

• Important: If $X$ loses a value, neighbors of $X$ need to be rechecked!
• Simple form of propagation that makes sure all arcs are consistent.
  • 
• $RemoveInconsistentValues$: $O(d^2)$
• $AC-3$: $O(d^3{n}^2)$

K-Consistency §

• Increasing degrees of consistency
• 1-Consistency (Node Consistency): Each single node’s domain has a value which meets that node’s unary constraints
• 2-Consistency (Arc Consistency): For each pair of nodes, any consistent assignment to one can be extended to another.
• K-Consistency: For each $k$ nodes, any consistent assignment to $k-1$ can be extended to the $k^{th}$ node.