Lecture 18 Bayesian Networks II

#notes#cs471

Recap §

• Set of nodes, one per random variable X
• Directed, acyclic graph
• A conditional distribution for each node
  • Collection of probability distributions over X, one for each combination of parents’ values.
• CPT: Conditional probability table
• Chain Rule, a product of conditional probabilities
  • $P(x_1,x_2,...,x_n)={\Pi }_{i=1}^{n}P(x_i|x_1...x_{i-1})$
• Assume conditional independence:
  • $P(x_i|x_1...x_{i-1})=P(x_i|parents(X_i))$

Causal chains

• Low pressure causes rain causes traffic.
• High pressure causes no rain causes no traffic
• P(x,y,z) = $P(x)P(y|x)P(z|y)$
• Can flip them and get same result

Bayesian Networks II §

D-Separation §

• Determine independence by checking triples

Common Cause §

• One event that causes 2 events.
• $P(x,y,z)=P(y)P(x|y)P(z|y)$
• A -> B, A -> C, A is the common cause.
• It is not guaranteed B is independent of C
• It is independent if we are given A,

Common Effect §

• A -> C, B -> C
• A and B are not independent given C.
• A and B ARE independent (if we are not given C)
• So, 2 causes of 1 effect
• Imagine backwards effect. Seeing C now makes A and B not independent as we can use C to explain A and B.

Active / Inactive Paths §

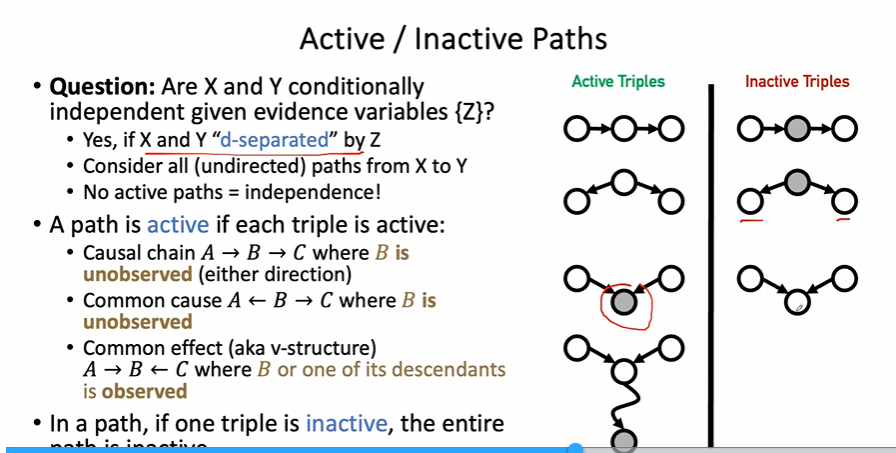
• If all paths inactive, then conditional independence.
• If one triple inactive, that path is active.
• Check multiple paths, if one is active, then variables are not independent.